

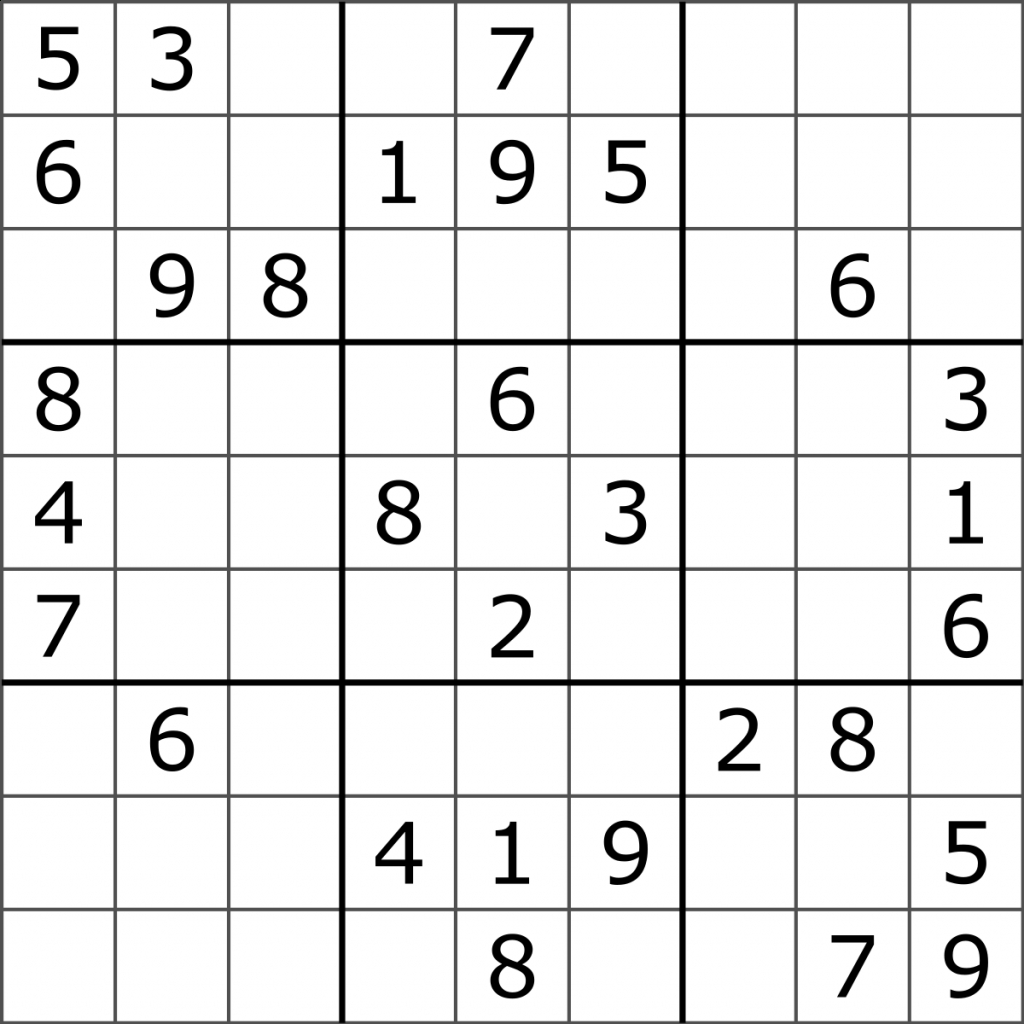
Solving 9x9 with 2 missing numbers using Quantum Computing.Sudoku is a logic puzzle game. Quantum Solving 4x4 with 4 missing numbers.ĮmptySquareEdges =
SudokuGroverSample.csproj: Main project for the sample. #Color sudoku solver code#
SudokuQuantum.cs: C# code to solve a Sudoku puzzle by transforming it into a graph problem (edges and starting number constraints), and call the Quantum SolvePuzzle operation to solve it.SudokuClassic.cs: C# code to solve a Sudoku puzzle using classical code.Sudoku.qs: Q# code which accepts edges and constraints and calls Grover's algorithm with the coloring oracle.Program.cs: C# code with Sudoku test problems to solve using classical or Quantum code.A custom oracle for coloring with only 9 colors is also implemented. ColoringGroverWithConstraints.qs: Q# code implementing graph coloring with flexible number of bits per color and ability to specify constraints on the colors found per Vertex.9x9-64: test classic algorithm and Quantum solution on aįor example, dotnet run 4x4-4 will run the Quantum solution for a 4x4 puzzle with 4 missing numbers Manifest.9x9-1: test classic algorithm and Quantum solution on a.4x4-4: test Quantum solution of 4x4 puzzle missing 4 numbers.4x4-3: test Quantum solution of 4x4 puzzle missing 3 numbers.4x4-1: test Quantum solution of 4x4 puzzle missing 1 number.4x4-classic : test classic algorithm on a 4x4 puzzle.You can also choose a specific puzzle to solve by adding the puzzle name as below
To run the sample, use the dotnet run command from your terminal.
for 9x9 puzzles, 4 bits per color are used but the colors in the solution can only be 0 to 8. constraints on Vertex colors based on initial colors when you start. The graph coloring code is based on the Graph Coloring Kata with the following changes: However, trying to use more than 8 qubits (2 empty squares) in a simulation becomes very slow, so here we only run it for 1 or 2 missing squares in a 9x9 puzzle. The code can also solve 9x9 Sudoku puzzles using 4 qubits per number. This allows a 4x4 puzzle to be solved using 2 qubits per missing number. The numbers are changed to 0 to 3 and 0 to 8 and then converted back. However, when solving this using a quantum program and encoding these values into qubits, Note that the puzzles are initially defined in C# using numbers from 1 to 4, or 1 to9. Similarly, startingNumberConstraints is the array of (Cell#, constraint).įor example, the constraint that empty cell 0 can't have value 1 or 3 is encoded as startingNumberConstraints =. A list of constraints on empty squares to the initial numbers in the puzzle (starting numbers)įor example, for the row above the empty squares have indices: _Īnd emptySquareEdges is the array of edges.įor example, cell 0 can't have the same number (color) as cell 1, so emptySquareEdges =. A list of edges connecting empty squares. We define the puzzle using 2 data structures. To reduce the number of qubits, we only use qubits for empty squares.Įach empty square gets 2 qubits to encode the numbers 0 to 3. In the above example, the constraints for the top row are _ Graph edges are the constraints preventing squares from having the same values. In our case, graph nodes are puzzle squares and colors are the Sudoku numbers. Sudoku is a graph coloring problem where graph edges must connect nodes of different colors. The numbers 0 to 3 may only appear once per row, column and 2x2 sub squares. 
The code supports both 4x4 and 9x9 Sudoku puzzles. This program demonstrates solving Sudoku puzzle using Grover's algorithm.







 0 kommentar(er)
0 kommentar(er)
